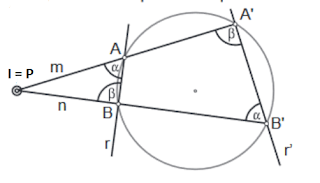
- Están alineados. P y P' (inverso de P) están alineados con I, centro de inversión.
- El producto de las distancias IP x IP' es constante e igual a la constante de inversión K2. Concepto de potencia.
PA x PA' = PB x PB' = PC x PC' = PT x PT' = K2
Por ello, todos los pares de puntos son inversos respecto del centro de inversión I = P.
A y A' son inversos, B y B' son inversos, C y C' son inversos y T es inverso de sí mismo. Es decir T = T', se dice que T es un punto doble.
La circunferencia con centro en el centro de inversión I=P y radio IT, sobre el dibujo anterior, es una circunferencia de puntos inversos de sí mismos, de puntos dobles, se llama circunferencia de autoinversión. Con el centro I y la circunferencia de autoinversión queda determinada la Inversión:
Las rectas m y n que pasan por A-A' y B-B' respectivamente, son antiparalelas a las rectas r y r' que pasan por A-B y A'-B' respectivamente.
INVERSIÓN POSITIVA E INVERSIÓN NEGATIVA
Dos circunferencias dadas son homotéticas respecto de dos centros, uno positivo y otro negarivo. Si se considera que una es inversa de la otra, los centros de homotecia se corresponden con los centros de inversión, el positivo I+ y el negativo I-.
Cuando la potencia es positiva, los puntos inversos T1+ y T1'+ se encuentran al mismo lado del centro de inversión I+. Cuando la potencia es negativa, los puntos inversos T2- y T2'- se encuentran uno a cada lado del centro de inversión I-. Se puede ver esto gráficamente en la figura siguiente.
Cuando la inversión es positiva, existen puntos dobles hay una circunferencia de autoinversión. Podemos obtenerla como en la figura.
Todas la circunferencias que pasan por T1+ y T1'+ contienen puntos inversos respecto de I+ por tener todos igual potencia respecto de I+ (concepto de potencia y de haz elíptico de circunferencias). La circunferencia mínima que pasa por T1+ y T1'+ también, podemos encontrar así el punto doble T = T' y la circunferencia de autoinversión.
Al dibujar la circunferencia que contiene los punto T2-, T2'-, F- y F'-, vemos que en dicha circunferencia no exitente puntos dobles posibles, cada punto y su inverso están siempre uno a cada lado del centro de inversión I-.
IMAGEN DE UNA RECTA MEDIANTE UNA INVERSIÓN.
De la definición de inversión, queda claro que la inversión de una recta que pasa por el centro de inversión es ella misma.
Como se ve en la figura, la recta a que pasa por AD es la misma que la recta inversa a' que pasa por los respectivos puntos inversios A'D'.
La imagen de una recta que NO pasa por el centro de inversión es una circunferencia que pasa por el centro de inversión.
Partimos de la circunferencia c que pasa por I centro de inversión. Obtenemos el inverso de Q, Q' por el teorema del cateto. El inverso del punto S (alineado con el centro de la circunferencia O), S' es concíclico con Q, Q' y S.
El ángulo IQS tiene que ser recto por estar inscrito en una semicircunferencia, ppor antiparalelismo, tenemos que el ángulo SS'Q' también ha de ser recto. Esta situación se da para todos los puntos Q-Q' que conforman la circunferencia c, luego, la imagen de la circunferencia c es la recta c'.
IMAGEN DE UNA CIRCUNFERENCIA QUE NO PASA POR EL CENTRO DE INVERSIÓN.
Como ya se ha mostrado más arriba, al hablar de circunferencias homotéticas, dos circunferencias homotéticas son inversas si se toman los centros de homotecia como centros de inversión.
Luego, la imagen de una circunferencia que no pasa por el centro de inversión es otra circunferencia que tampoco pasa por el centro de inversión.
Se proponen los siguientes ejercicios de inversión directa.
Ejercicio 1 de inversión directa. Circunferencias concéntricas.
Ejercicio 2 de inversión directa (variante del ejercicio 1). Circunferencias concéntricas.
Referencias:
laslaminas
piziadas